Каморка

... решить неординарно

Что такое сферический РАД и сколько их в шаре? Но это не задача- это начало Wanted не только знания, но и пространственное воображение.

... а женщины тут причем? ... это в Игрульки ... или там что-то дальше женское ...

Gatchinskiy писал(а):... а женщины тут причем? ... это в Игрульки ... или там что-то дальше женское ...

Поместив этот топик сюда, я надеюсь получить неординарный ответ. Это не означает, что мужчины не должны принимать участия

Да, ребята-девчата С радианами у нас труба. Жаль.

По аналогии с обычным радианом. Но прикладывать его придется на 4х мерную сферу. ОТО балуемся?

Стерадиан равен телесному углу с вершиной в центре сферы, вырезающему на поверхности сферы площадь, равную площади квадрата, со стороной, равной радиусу сферы. Если такой телесный угол имеет вид конуса, то угол его раскрытия составит 65°32′28″.
Площадь поверхности сферы 4*Pi*R*R, соответственно в сфере 4*Pi стерадиан.

runner писал(а):По аналогии с обычным радианом. Но прикладывать его придется на 4х мерную сферу. ОТО балуемся?

На 3х мерную - стерадиан не относится к ОТО.

Stanislav писал(а):

runner писал(а):По аналогии с обычным радианом. Но прикладывать его придется на 4х мерную сферу. ОТО балуемся?

На 3х мерную - стерадиан не относится к ОТО.

Ну, значит, перепутал...

Что такое сферический РАД и сколько их в шаре? icon_lol.gif

ЭЭЭЭ.....может лучше про продажных тётак?

oblom писал(а):

Что такое сферический РАД и сколько их в шаре? icon_lol.gif

ЭЭЭЭ.....может лучше про продажных тётак?

ну что ты так приземленно праздник на дворе пусть народ развлекается

Stanislav писал(а): Если такой телесный угол имеет вид конуса, то угол его раскрытия составит 65°32′28″.

Это самое ценное, что нужно А может этот телесный угол иметь НЕ форму конуса? Иными словами, в основании вырезанной фигуры лежит не круг (хотя и в первом случае не круг, а как он называется, сферический сегмент ?), а все, что угодно? Спасибо, Stanislav

Bora писал(а):

Stanislav писал(а): Если такой телесный угол имеет вид конуса, то угол его раскрытия составит 65°32′28″.

Это самое ценное, что нужно А может этот телесный угол иметь НЕ форму конуса? Иными словами, в основании вырезанной фигуры лежит не круг (хотя и в первом случае не круг, а как он называется, сферический сегмент ?), а все, что угодно? Спасибо, Stanislav

Да, конечно. Смысл в том, какую площадь он отсекает на сфере, а не его форма.

Stanislav писал(а):

Bora писал(а):

Stanislav писал(а): Если такой телесный угол имеет вид конуса, то угол его раскрытия составит 65°32′28″.

Это самое ценное, что нужно А может этот телесный угол иметь НЕ форму конуса? Иными словами, в основании вырезанной фигуры лежит не круг (хотя и в первом случае не круг, а как он называется, сферический сегмент ?), а все, что угодно? Спасибо, Stanislav

Да, конечно. Смысл в том, какую площадь он отсекает на сфере, а не его форма.

Ну и соответственно при равной отсеченной площади на поверхности сферы получаются равно отсеченные объемы в сфере, да?

Я усекла усечение, спасибо, Вы ценная находка.

Bora писал(а):Ну и соответственно при равной отсеченной площади на поверхности сферы получаются равно отсеченные объемы в сфере, да?
Я усекла усечение, спасибо, Вы ценная находка.

Истинно так!

Bora писал(а):

Stanislav писал(а): Если такой телесный угол имеет вид конуса, то угол его раскрытия составит 65°32′28″.

Это самое ценное, что нужно А может этот телесный угол иметь НЕ форму конуса? Иными словами, в основании вырезанной фигуры лежит не круг (хотя и в первом случае не круг, а как он называется, сферический сегмент ?), а все, что угодно? Спасибо, Stanislav

Бора может даже треугольник там лежать и будет он сферический треугольник


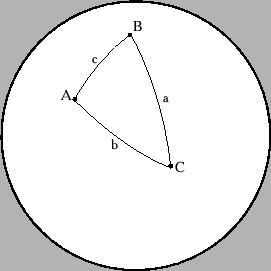
вот почитай как его площадь через сферические радианы посчитать
http://www.astronet.ru/db/msg/1190894/node7.html