Что такое сферический РАД и сколько их в шаре?
Wanted!
Правила форума
Пожалуйста, ознакомьтесь с правилами данного форума
Пожалуйста, ознакомьтесь с правилами данного форума
- Gatchinskiy
- Комбинатор
- Сообщения: 20952
- Зарегистрирован: 05 окт 2003, 20:44
- Откуда: St. Petersburg(Gatchina) > Vancouver
- Bora
- Житель
- Сообщения: 613
- Зарегистрирован: 06 ноя 2005, 19:11
- Bora
- Житель
- Сообщения: 613
- Зарегистрирован: 06 ноя 2005, 19:11
- Проф. Преображенский
- Графоман
- Сообщения: 20276
- Зарегистрирован: 08 ноя 2006, 11:10
- Stanislav
- Mr. Minority Report
- Сообщения: 46101
- Зарегистрирован: 19 окт 2005, 16:33
- Откуда: Moscow - Richmond - New Wesт - Burnaby - PoCo
Стерадиан равен телесному углу с вершиной в центре сферы, вырезающему на поверхности сферы площадь, равную площади квадрата, со стороной, равной радиусу сферы. Если такой телесный угол имеет вид конуса, то угол его раскрытия составит 65°32′28″.
Площадь поверхности сферы 4*Pi*R*R, соответственно в сфере 4*Pi стерадиан.
Площадь поверхности сферы 4*Pi*R*R, соответственно в сфере 4*Pi стерадиан.
- Stanislav
- Mr. Minority Report
- Сообщения: 46101
- Зарегистрирован: 19 окт 2005, 16:33
- Откуда: Moscow - Richmond - New Wesт - Burnaby - PoCo
- Проф. Преображенский
- Графоман
- Сообщения: 20276
- Зарегистрирован: 08 ноя 2006, 11:10
-
oblom
- Читатель
- Сообщения: 10786
- Зарегистрирован: 20 фев 2003, 22:04
- Vims
- Northern Yeti
- Сообщения: 21479
- Зарегистрирован: 17 фев 2003, 15:53
- Откуда: Magadan - Vancouver
- Контактная информация:
- Bora
- Житель
- Сообщения: 613
- Зарегистрирован: 06 ноя 2005, 19:11
Это самое ценное, что нужноStanislav писал(а): Если такой телесный угол имеет вид конуса, то угол его раскрытия составит 65°32′28″.
- Stanislav
- Mr. Minority Report
- Сообщения: 46101
- Зарегистрирован: 19 окт 2005, 16:33
- Откуда: Moscow - Richmond - New Wesт - Burnaby - PoCo
Да, конечно. Смысл в том, какую площадь он отсекает на сфере, а не его форма.Bora писал(а):Это самое ценное, что нужноStanislav писал(а): Если такой телесный угол имеет вид конуса, то угол его раскрытия составит 65°32′28″.А может этот телесный угол иметь НЕ форму конуса? Иными словами, в основании вырезанной фигуры лежит не круг (хотя и в первом случае не круг, а как он называется, сферический сегмент ?), а все, что угодно?
Спасибо, Stanislav
- Bora
- Житель
- Сообщения: 613
- Зарегистрирован: 06 ноя 2005, 19:11
Ну и соответственно при равной отсеченной площади на поверхности сферы получаются равно отсеченные объемы в сфере, да?Stanislav писал(а):Да, конечно. Смысл в том, какую площадь он отсекает на сфере, а не его форма.Bora писал(а):Это самое ценное, что нужноStanislav писал(а): Если такой телесный угол имеет вид конуса, то угол его раскрытия составит 65°32′28″.А может этот телесный угол иметь НЕ форму конуса? Иными словами, в основании вырезанной фигуры лежит не круг (хотя и в первом случае не круг, а как он называется, сферический сегмент ?), а все, что угодно?
Спасибо, Stanislav
Я усекла усечение, спасибо, Вы ценная находка.
- Stanislav
- Mr. Minority Report
- Сообщения: 46101
- Зарегистрирован: 19 окт 2005, 16:33
- Откуда: Moscow - Richmond - New Wesт - Burnaby - PoCo
- дядя Вова
- Графоман
- Сообщения: 5603
- Зарегистрирован: 09 июн 2005, 15:09
- Откуда: Батуми-Одесса
Бора может даже треугольник там лежать и будет он сферический треугольникBora писал(а):Это самое ценное, что нужноStanislav писал(а): Если такой телесный угол имеет вид конуса, то угол его раскрытия составит 65°32′28″.А может этот телесный угол иметь НЕ форму конуса? Иными словами, в основании вырезанной фигуры лежит не круг (хотя и в первом случае не круг, а как он называется, сферический сегмент ?), а все, что угодно?
Спасибо, Stanislav
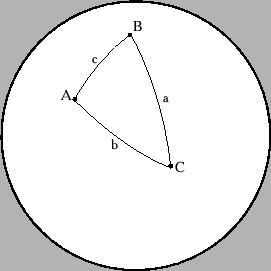
вот почитай как его площадь через сферические радианы посчитать
http://www.astronet.ru/db/msg/1190894/node7.html